In one of my recent project, I need to implement a lock service for files. It is quite similar to the lock service of existing file systems. I need to support two modes: write (exclusive) and read (shard). For instance, “R/a/b/c” means a read lock for the file with path “/a/b/c”. Likewise, “W/a/b/c” stands for a write lock.
The interface is pretty straightforward. The user provide a set of locks, e.g., {R/a/b/c, R/a/b/d}, to be locked by our service. One challenge we face is to deduplicate the locks given by the user. For instance, the user may provide a set of locks {R/a/b/c, W/a/b/c}. In this example, we know the write lock is stronger than the read lock, and therefore, the set is equivalent to {W/a/b/c}. We tend to reduce the number of locks, since it is beneficial for checking less conflicts in the steps afterwards.
So far, the deduplication problem sounds quite simple, since we only need to consider locks with exactly the same path. However, we also need to support a wildcard notation, because we have a large number of files under one directory. If we want to lock all files in this directory, we need to generate a huge list of locks, each for a file. With a wildcard, we lock all files under “/a/b/“ with “R/a/b/*”. The wildcard makes the deduplication problem much more complicated.
We first clarify the coverage of locks by a concrete example:
1 | W/a/b/* > W/a/b/c > R/a/b/c |
Given a large set of locks, a very simple algorithm is that we compare each pair of locks. If one is stronger than the other, the weaker one is throw away. The result set contains only locks where no one is stronger than other locks. This algorithm’s complexity is O(n*n) which is slow if the given set is large. So, I try to find a faster algorithm.
After some thoughts, I developed an algorithm with complexity O(n), which constructs a tree on the set of locks. Each tree node has the following attributes:
1 | class Node { |
We now explain how to construct a lock tree with a concrete example.
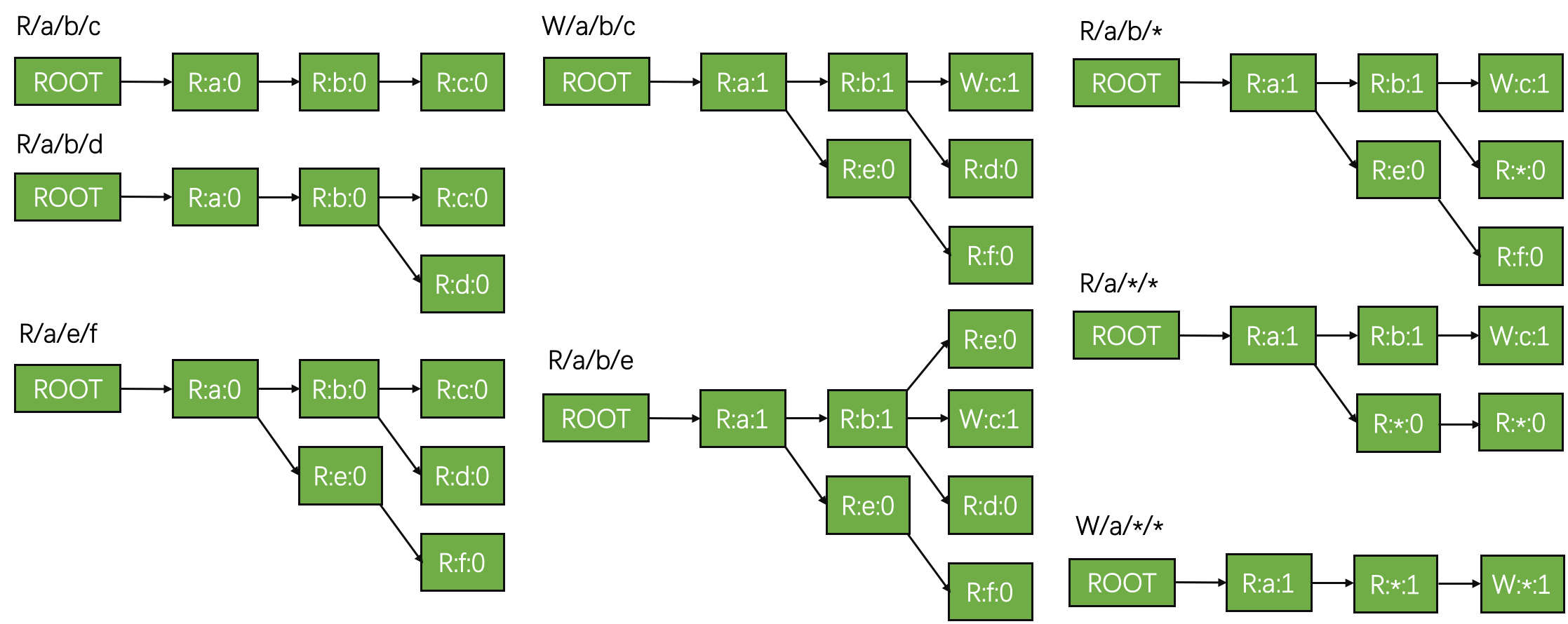
In the figure above, we show inserting a set of locks into an empty lock tree. Each node is represented with a string “mode:name:mark”.
Step 1~3: Inserting the first three locks {R/a/b/c, R/a/b/d, R/a/e/f} is straightforward.
Step 4: Then, inserting the 4th lock, i.e., “W/a/b/c”, has two effects: (1) upgrade the original “R” lock of /a/b/c to “W” mode; (2) mark the path of “/a/b/c” from 0 to 1.
Step 5: The 5th lock “R/a/b/e” is the same with the first three.
Step 6~7: Then, the 6th lock “R/a/b/*“ contains a wildcard. Having a “R” wildcard means replacing all unmarked nodes (“R:e:0” and “R:d:0”) with a “R:*:0” node, in its parent’s subtree (the parent is “R:b:1” in this case). Similarly, inserting “R/a/*/*“ first removes all unmarked nodes in “R:a:1”‘s subtree, i.e., “R:e:0”, “R:*:0”, and “R:f:0”, and then insert new nodes with wildcard.
Step 8: Finally, inserting a “W” mode lock with wildcard means deleting all nodes in the subtree of “R:a:1” (the wildcard node’s parent) and then insert the new nodes.
After constructing the lock tree, each path from root to leaf is a lock in our deduplicated result set. In practice, a hashmap may already solve most duplicated cases. We rarely encounter extreme cases as shown in the example above. The algorithm briefly described above is only for fun :). I didn’t mention paths with different lengths since they could be put into different trees, which is therefore not a real problem.
I didn’t elaborate all cases in the example above, which is more complicated. A sample implementation of the algorithm could be find here. The output is as follows:
1 | R/a/b/c |